|
|
|
|
|
|
|
|
In einer Stichprobe aus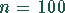 
Personen befinden sich 
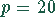% Raucher. Wie groß ist der Vertrauensbereich
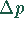, wenn dieser Prozentsatz mit 95 % Wahrscheinlichkeit für die Grundgesamtheit
aller Personen zu trifft?
In dem gegebenen Fall liegt eine diskrete Binomialverteilung vor. Der Vertrauensbereich berechnet sich nach
Voraussetzung ist, daß der Stichprobenumfang n der Bedingung
genügt. Für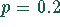 
folgt die Bedingung
Der Stichprobenumfang von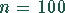 
genügt dieser Bedingung. Für große Grundgesamtheiten
und Stichprobenmengen geht die Binomialverteilung in die Normalverteilung über.
Mit dieser läßt sich einfacher rechnen. Für eine Normalverteilung gilt für eine
95 %ige Wahrscheinlichkeit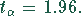 
Diese Größe kann man aus einer Statistiktabelle für die standardisierte Normalverteilung entnehmen, oder man nutzt ein Mathematikprogramm wie
Mathematika
Needs["Statistics`Master`"] verteil=NormalDistribution[0,1] N[Quantile[verteil,0.99]]Damit ergibt sich als Vertrauensbereich für den Prozentsatz der Raucher in der Grundgesamtheit
Der Prozentsatz der Raucher liegt mit 95 % Wahrscheinlichkeit zwischen 12.16 % und 27.84 % .
Wie groß müßte der Stichprobenumfang mindestens sein, wenn der Anteil der Raucher 5 % wäre? Aus der Bedingung für die Anwendbarkeit der Normalverteilung folgt
Bei einem Anteil der Raucher in der Stichprobe von 5 % müßten mindestens 190 Personen in der
Stichprobe erfaßt werden.
