|
|
|
|
|
|
|
|
-Funktion, summierte Quadrate von n Meßwerten
einer Stichprobe
-Verteilung ( Helmert-Pearson),
Verteilung 
, die sich
für die Meßgröße
mit
ergibt, wenn die einzelnen Meßwerte 
jeweils
standardnormalverteilt sind
Der Parameter der Verteilung ist der Stichprobenumfang n.
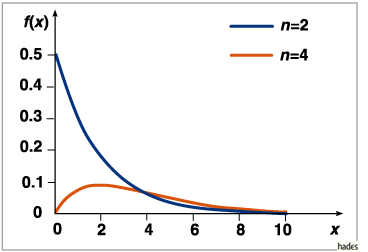
Die n Meßwerte 
können, wenn sie einer
allgemeineren Normalverteilung um den bekannten
Erwartungswert m mit der
Varianz 
gehorchen, auch
ersetzt werden durch
Die Verteilung von 
ist ebenso 
.
Ist der Erwartungswert m nicht bekannt, kann er durch
das arithmetische Mittel der Probe 
ersetzt werden.
Die Verteilung von 
ist dann jedoch 
.
Der Wert
ist eine Schätzfunktion für
die Varianz (mittlere quadratische Abweichung), sofern
normalverteilt um m.
Die Perzentile der 
-Verteilung 
mit
werden im Rahmen der Schätztheorie zur
Definition der Prognose- und Konfidenzintervalle bei der
Intervallschätzung von Varianz-Parametern 
bei Normalverteilung verwendet. Hierbei dient 
als Schätzer.
Analog dazu werden in der Testtheorie
solche Perzentile ebenfalls zur Bestimmung der
Güte eines geschätzten 
-Wertes herangezogen.
|
|
|
|
|
|
|
|
,