|
|
|
|
|
|
|
|
Eine Werbeagentur möchte überprüfen, wie stark sie die Leser einer Zeitung mit einer
Auflage von 10000 Stück durch ihre Anzeige angesprochen haben. Dazu werden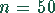 
verschiedene, zufällig ausgewählte Leser befragt, ob sie die Anzeige gelesen haben.
Von den Befragten haben 15 die Anzeige gelesen. Mittels des
Maximum-Likelihood-Verfahrens schätzt man ab, daß etwa
d.h. 30 % der Leser die Anzeige gelesen haben. Das Konfidenzintervall beträgt
Die Größe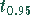 
kann man aus einer Statistiktabelle für die standardisierte
Normalverteilung entnehmen, oder man nutzt ein Mathematikprogramm wie
Mathematika
Needs["Statistics`Master`"] verteil=NormalDistribution[0,1] N[Quantile[verteil,0.95]]Mit 95 % Wahrscheinlichkeit liegt die Zahl der Leser, die die Anzeige gelesen haben, zwischen 19.23 % und 40.7 % aller Leser.
Wie groß hätte der Stichprobenumfang liegen müssen, damit mit einer 97 %-Sicherheit der Anteil der Leser, die die Anzeige gelesen haben, in einem symmetrischen Konfidenzintervall der Breite 6 % um den Anteilswert p liegen soll, wenn man keine Information über den Wert besitzt?
Der Stichprobenumfang kann nach der Beziehung
berechnet werden. Da p nicht bekannt ist, muß man p abschätzen. Es geht
in diesem Fall darum, einen unteren Wert für die Stichprobengröße zu finden.
Der größte Wert wird erhalten, wenn 
ein Maximum hat. Damit kann ein
Wert errechnet werden, der auf der sicheren Seite liegt.
Die Funktion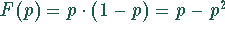 
hat ihr Maximum an der Stelle, wo ihre
erste Ableitung null ist. Das ergibt
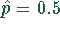. Da das Konfidenzintervall 
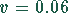ist, ergibt sich für die
Stichprobengröße:
