|
|
|
|
|
|
|
|
Parametertest bei der Normalverteilung
Ein Hersteller von Glühlampen garantiert seinen Kunden eine mittlere Lebensdauer von 1400 Betriebsstunden. Die Standardabweichung beträgt 60 Stunden. Zur Überprüfung der Herstellerangaben entnimmt eine Verbraucherorganisation einer sehr großen Lieferung eine Stichprobe von 100 Glühlampen. Sie stellen eine mittlere Lebensdauer von 1388 Stunden fest.
Muß diese Lieferung mit einer Irrtumswahrscheinlichkeit von 5 % abgelehnt werden oder nicht?
Da eine Abweichung vom Sollwert 
h nach beiden Richtungen zugelassen
ist, spricht man von einer zweiseitigen Fragestellung.
Die Lebensdauer einer Glühlampe ist auf Grund des Produktionsprozesses eine
normalverteilte Zufallsvariable mit dem Erwartungswert 
h und der
Varianz 
.
Siehe die Abbildung
Die Nullhypothese lautet:
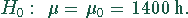
Als Alternativhypothese 
wählt man alle möglichen Abweichungen
von 
, d.h.,
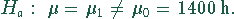
Um die Nullhypothese zu testen,
muß die Stichprobenfunktion 
so
normiert werden, daß man eine Zufallsvariable erhält, die einer standardisierten
Normalverteilung entspricht. Dies erfolgt durch die Transformation
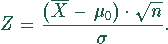
Man wird die Nullhypothese ablehnen, wenn der Betrag dieser normierten Zufallsvariablen für die Stichprobenrealisation
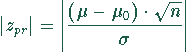
in einem kritischen Bereich 
liegt,
der symmetrisch um den Mittelwert 
liegt und so konstruiert ist, daß dies nur
mit der vorgegebenen Irrtumswahrscheinlichkeit
eintreffen wird.
Für die transformierte Stichprobenrealisation erhält man
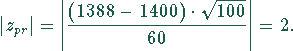
Der kritische Wert für die Zufallsvariable bei einer Irrtumswahrscheinlichkeit liefert das Perzentil
Da der Betrag der Prüfgröße 
ist (
), ist die
Nullhypothese abzulehnen. Das bedeutet, die Lieferung von Glühlampen
entspricht hinsichtlich ihrer Lebensdauer nicht dem vom Lieferbetrieb
garantierten Wert.
Der Wert des Perzentils kann aus einer Tabelle für die Verteilungsfunktion der standardisierten Normalverteilung entnommen werde. Eine Möglichkeit bietet auch das Programm Mathematica.
Mathematica
Needs["Statistics`Master`"] verteil=NormalDistribution[0,1] N[Quantile[verteil,0.99]]
Kürzer erhält man diese Aussage unter Verwendung der Formel in dem Taschenbuch für einen zweiseitigen Test.
Die Nullhypothese muß abgelehnt werden, wenn
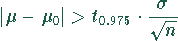
gilt. In dem vorliegenden Fall ergibt sich
