Extremwertsuche

 restart;
 readlib(extrema):
 f=x->              ;# (* Funktion eingeben *)
 extrema(f(x),{ }, x, lsg);

Bei komplizierten Funktionen müssen die Nullstellen der ersten Ableitungen numerisch gefunden werden. Dann muß eine andere Befehlsfolge benutzt werden. Zuvor ist die Funktion graphisch darzustellen, um die ungefähre Lage der Extremwerte zu bestimmen. Aus der Graphik bestimmt man Anfang und Ende des x- Bereiches empirisch. Die ungefähre Lage der Extremwerte kann durch Anklicken dieser Werte in der Kurve mittels der Maus oben links abgelesen werden.

1.Schritt:

restart;
f:=               ;   # (* Funktion eingeben *)
xstart:=              ;
xende:=               ;
plot(f(x),x=xstart..xende);

2.Schritt (Extremwertsuche und -berechnung):

Die aus der graphischen Darstellung folgenden Bereiche in denen ein Extremwert liegt müssen in der unten mit

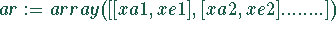
bezeichneten zweispaltigen Matrix eingetragen werden. Dabei ist xa1 der Anfang des Bereiches in dem der erste Extremwert liegt und xe1 das Ende dieses Bereiches.

#(* Bereichsgrenzen eintragen *)
ar:=array([[xa1,xe1],[xa2,xe2],[xa3,xe3],[xa4,xe4],..]);
n:=    :# (* Zahl der Extremwerte eingeben*)
f1:=unapply(diff(f(x),x),x);
for i from 1 to n do:
lr[ i] :=fsolve(f1(x),x,x=ar[i,1]..ar[i,2]): od:
f2:=unapply(diff(f1(x),x),x);
`* Lage der Extremwerte *`;
for j from 1 to n do:
if f2( lr[j])<0 then ex:=`Maximum` else ex:=`Minimum` fi:
print(ex);printf(`Lage:`): print( lr[j]):printf(`Wert:`):print(f(lr[j])):od:



#(* Beispiel *)
f:=x->x+2*sin(x);
plot(f(x),x=-5..5);
ar:=array([[-4.5,-3.5],[-2.5,-1.5],[1.5,2.5],[3.5,4.5]]);
n:= 4   :# (* Zahl der Extremwerte eingeben*)
f1:=unapply(diff(f(x),x),x);
for i from 1 to n do: lr[i]:=fsolve(f1(x),x,x=ar[i,1]..ar[i,2]):
od:
f2:=unapply(diff(f1(x),x),x);
`* Lage der Extremwerte *`;
for j from 1 to n do:
if f2(lr[j])<0 then ex:=`Maximum` else ex:=`Minimum` fi:
print(ex); printf(`Lage:`):print(lr[j]):printf(`Wert:`):
print(f(lr[j])):
od: