Divergenz

Kartesische Koordinaten:

restart:
with(linalg):
fx:=           :#(* x-Komponente der Vektorfunktion eingeben *)
fy:=           :#(* y-Komponente der Vektorfunktion eingeben *)
fz:=           :#(* z-Komponente der Vektorfunktion eingeben *)
v:=vector([fx,fy,fz]):
d:=diverge(v,[x,y,z]);

Beispiel:

Für ein Vektorfeld

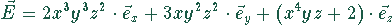
ist die Divergenz zu bilden

restart:
with(linalg):
fx:=2*x^3*y^3*z^2           :#(* x-Komponente der Vektorfunktion eingeben *)
fy:=3*x*y^2*z^2           :#(* y-Komponente der Vektorfunktion eingeben *)
fz:=x^4*y*z           :#(* z-Komponente der Vektorfunktion eingeben *)
v:=vector([fx,fy,fz]):
d:=diverge(v,[x,y,z]);

Sphärische Koordinaten:

restart:
with(linalg):
fr:=           :#(* Radialkomponente der Vektorfunktion eingeben *)
ft:=           :#(* Theta-Komponente der Vektorfunktion eingeben *)
fp:=           :#(* Phi-Komponente der Vektorfunktion eingeben *)
v:=vector([fr,ft,fp]):
d:=diverge(v,[r,theta,phi],coords=spherical);

Beispiel: Ein Dipol der Dipolstärke 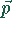erzeugt am Punkt r ein elektrisches Feld

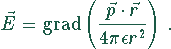
Das liefert die Divergenz:

restart:
with(linalg):
v:=grad(p*r*cos(theta)/(2*Pi*eps*r^2),[r,theta,phi],coords=spherical);
d:=  diverge( v,[ r, theta, phi] , coords=spherical);

Zylindrische Koordinaten:

restart:
with(linalg):
fr:=           :#(* Radialkomponente der Vektorfunktion eingeben *)
ft:=           :#(* Theta-Komponente der Vektorfunktion eingeben *)
fz:=           :#(* z-Komponente der Vektorfunktion eingeben *)
v:=vector([fr,ft,fz]):
d:=diverge(v,[r,theta,z],coords=cylindrical);