Differentialgleichung mittels Laplacetransformation lösen

restart:
dgl:=a*diff(diff(y(t),t),t)+b*diff(y(t),t)+c*y(t)=f(t):
`(* Lineare Differentialgleichung einer Funktion y(t) *)`:
a:=     :# (* Parameter eingeben *)
b:=     :# (* Parameter eingeben *)
c:=     :# (* Parameter eingeben *)
f(t):=  :# (* Inhomogaenitaet *)
dgl;
y0:=    :   # (*  Randbedingungen bzw. Anfangsbedingungen y(0) *)
y10:=   :   # (* Randbedingungen bzw. Anfangsbedingungen y'(0) usw.*)
alias(Y(s)=laplace( y(t),t,s)):
laplace(dgl,t,s);
lsg:=solve(subs(y(0)=y0,D(y)(0)=y10," ),Y(s));
y(t):=invlaplace(lsg,s,t)     ;
`(* Graphische Darstellung der Lösung *)`:
plot(y(t),t=0..10);

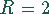Beispiel: Stromkreis mit Widerstand, Spule und Kondensator (siehe auch Beispiel 2 , Induktivität Henry, Widerstand Ohm, Kapazität Farad)

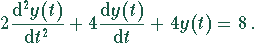
restart:
dgl:=a*diff(diff(y(t),t),t)+b*diff(y(t),t)+c*y(t)=f(t):

`(* Lineare Differentialgleichung einer Funktion y(t) *)`:
a:= 2     :
b:= 4    :
c:=  4   :
f(t):=8  :
dgl;
y0:= 0:    `(*  Randbedingungen bzw. Anfangsbedingungen y(0) *)`:
y10:=0:    `(* Randbedingungen bzw. Anfangsbedingungen y'(0) usw.*) `:
alias(Y(s)=laplace( y(t),t,s)):
laplace(dgl,t,s);
lsg:=solve(subs(y(0)=y0,D(y)(0)=y10," ),Y(s));
y(t):=invlaplace(lsg,s,t)     ;
`(* Graphische Darstellung der Lösung *)`:
plot(y(t),t=0..10);