Potenzreihenentwicklung
Funktionen lassen sich innerhalb bestimmter Grenzen durch Potenzreihen approximieren. Je mehr Glieder
einer Entwicklung hinzugenommen werden, desto besser ist die erreichte Annäherung. An bestimmten
Stellen und außerhalb des zulässigen Bereichs ist divergentes Verhalten zu erwarten.
Natürlicher Logarithmus
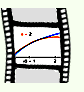
ln(x) wird im Intervall (0, 2] durch die Reihenentwicklung
ln(x) = 0 + (x-1) - (x-1)2/2 + (x-1)3/3 - (x-1)4/4 +-...
dargestellt.
Insbesondere oberhalb des geforderten Intervalls divergiert die Folge.

Wurzelfunktion
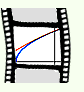
(1+x)1/2 wird im Intervall [-1, 1] durch die Reihenentwicklung
(1+x)1/2 = 1 + x · 1/2 - x2 · 1/8 +
x3 · 3/48 - x4 · 15/384 +-...
dargestellt.
Die Konvergenz ist sehr gut, da die Potenzfaktoren schnell gegen Null konvergieren.

Reziproke Funktion
(1+x)-1 wird im Intervall [-1, 1] durch die Reihenentwicklung
(1+x)-1 = 1 - x + x2 - x3 + x4 -+...
und für x>1 durch
(1+x)-1 = x-1 - x-2 + x-3 +- ...
dargestellt. (Für x>1 wurde nicht nach Potenzen von x, sondern nach Potenzen von 1/x
entwickelt.)
An der Stelle x = 1 divergieren beide Reihenentwicklungen.

















