|
|
|
|
|
|
|
|
konvergiert immer
an der Entwicklungsstelle 
, der triviale Fall 
.
Konvergenzradius r um die
Entwicklungsstelle kann angegeben werden, wenn die Reihe auch für
Werte ungleich 
konvergiert.
Konvergenzradius r der Potenzreihe, die kleinste obere
Schranke (Supremum) der Zahlen 
, für die
konvergiert. Dabei gilt: 
.
Die Reihe divergiert für alle x-Werte mit 
.
Konvergenzbereich, das symmetrische Intervall 
um die Entwicklungsstelle 
.
Konvergenzaussagen:
Formeln zur Berechnung des Konvergenzradius r:
Quotientenkriterium ergibt für
den Konvergenzradius r:
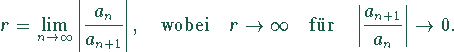
Diese Formel kann em nicht immer angewendet werden, obwohl das
Quotientenkriterium erfüllt ist.
Jedes zweite 
sei gleich null, 
ist nicht
definiert!.
Wurzelkriterium ergibt für den
Konvergenzradius r:
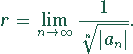
Die Formeln können nur dann benutzt werden, wenn der jeweilige
Grenzwert existiert. Existieren beide, dann stimmen die
Ergebnisse für r überein.
|
|
|
|
|
|
|
|
