Elementare Äquivalenzumformungen
1. Vertauschung der Seiten einer Gleichung
 Vertauscht man die Seiten einer Gleichung, so ist die neue Gleichung
der alten äquivalent.
Vertauscht man die Seiten einer Gleichung, so ist die neue Gleichung
der alten äquivalent.

 und
und 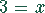 sind äquivalente Gleichungen.
sind äquivalente Gleichungen.
 Bei Ungleichungen ist dies nicht gültig!
Bei Ungleichungen ist dies nicht gültig!
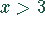 und
und 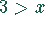 sind einander nicht äquivalent, sie widersprechen sich
sogar.
sind einander nicht äquivalent, sie widersprechen sich
sogar.
2. Termaddition und -subtraktion
 Addiert oder subtrahiert man auf beiden Seiten einer Gleichung
jeweils den gleichen Term, so sind alte und neue Gleichung äquivalent.
Addiert oder subtrahiert man auf beiden Seiten einer Gleichung
jeweils den gleichen Term, so sind alte und neue Gleichung äquivalent.

 und
und 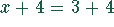 bzw.
bzw. 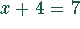 sind äquivalent.
sind äquivalent.
 und
und 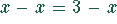 bzw.
bzw. 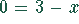 sind äquivalent.
sind äquivalent.
3. Termmultiplikation und -division
 Multipliziert oder dividiert man auf beiden Seiten einer Gleichung
jeweils den gleichen Term, der aber nicht Null sein darf,
so sind alte und neue Gleichung äquivalent.
Multipliziert oder dividiert man auf beiden Seiten einer Gleichung
jeweils den gleichen Term, der aber nicht Null sein darf,
so sind alte und neue Gleichung äquivalent.

 und
und  bzw.
bzw.  sind äquivalent.
sind äquivalent.
 und
und 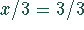 bzw.
bzw. 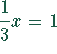 sind äquivalent.
sind äquivalent.
 Vorsicht beim Multiplizieren oder Dividieren mit Termen, die die
Variable selbst enthalten.
Vorsicht beim Multiplizieren oder Dividieren mit Termen, die die
Variable selbst enthalten.

 und
und 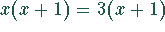 bzw.
bzw. 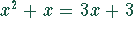 sind nur dann äquivalent,
wenn für die zweite Gleichung
sind nur dann äquivalent,
wenn für die zweite Gleichung 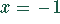 als mögliche Lösung
explizit ausgeschlossen wird.
als mögliche Lösung
explizit ausgeschlossen wird.
 und
und 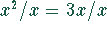 bzw.
bzw.  . Die Division durch x ist nur
zulässig, wenn
. Die Division durch x ist nur
zulässig, wenn  ausgeschlossen ist, d.h.
ausgeschlossen ist, d.h.  als Lösung von
als Lösung von
 vor der Division bekannt war. Erst dann sind
vor der Division bekannt war. Erst dann sind  und
und  äquivalent.
äquivalent.
4. Substitution
 Substituiert man einen Term durch eine neue Variable, so erhält man die
Lösung der ursprünglichen Gleichung, wenn man die neue Gleichung löst und
anschließend rücksubstituiert.
Substituiert man einen Term durch eine neue Variable, so erhält man die
Lösung der ursprünglichen Gleichung, wenn man die neue Gleichung löst und
anschließend rücksubstituiert.

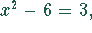 Substitution
Substitution 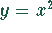
neue Gleichung 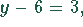 Lösung:
Lösung: 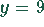 ,
,
Rücksubstitution 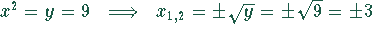 .
.















 Vertauscht man die Seiten einer Gleichung, so ist die neue Gleichung
der alten äquivalent.
Vertauscht man die Seiten einer Gleichung, so ist die neue Gleichung
der alten äquivalent.

 Bei Ungleichungen ist dies nicht gültig!
Bei Ungleichungen ist dies nicht gültig!  Addiert oder subtrahiert man auf beiden Seiten einer Gleichung
jeweils den gleichen Term, so sind alte und neue Gleichung äquivalent.
Addiert oder subtrahiert man auf beiden Seiten einer Gleichung
jeweils den gleichen Term, so sind alte und neue Gleichung äquivalent.

 Multipliziert oder dividiert man auf beiden Seiten einer Gleichung
jeweils den gleichen Term, der aber nicht Null sein darf,
so sind alte und neue Gleichung äquivalent.
Multipliziert oder dividiert man auf beiden Seiten einer Gleichung
jeweils den gleichen Term, der aber nicht Null sein darf,
so sind alte und neue Gleichung äquivalent.

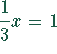 sind äquivalent.
sind äquivalent.
 Vorsicht beim Multiplizieren oder Dividieren mit Termen, die die
Variable selbst enthalten.
Vorsicht beim Multiplizieren oder Dividieren mit Termen, die die
Variable selbst enthalten.

 Substituiert man einen Term durch eine neue Variable, so erhält man die
Lösung der ursprünglichen Gleichung, wenn man die neue Gleichung löst und
anschließend rücksubstituiert.
Substituiert man einen Term durch eine neue Variable, so erhält man die
Lösung der ursprünglichen Gleichung, wenn man die neue Gleichung löst und
anschließend rücksubstituiert.








