Zahlenarten

Integer , exakte ganze Zahl beliebiger Länge, Eingabe in der Form nnnnn.

Rational ,  rationale Zahl (teilerfremder Bruch der Form Integer/Integer ), Eingabe in der Form ppppp/qqqqq.

Real ,  reelle Gleitpunktzahl von beliebiger zu spezifizierender Präzision, Eingabe in der Form nnnnn.mmmmm.

Complex ,  komplexe Zahl der Form Zahl+ Zahl I , wobei die reellen und imaginären Komponenten einem beliebigen Zahlentyp angehören können.

Testoperationen, geben Auskunft über Zahlen bzw. Ausdrücke:

Head[x]

stellt den Typ einer Zahl x fest und gibt ihn aus.

NumberQ[x]

liefert den Booleschen Wert True oder False für den Fall, daß x eine Zahl ist oder nicht. Ähnliche Tests (selbsterklärend): IntegerQ[x], EvenQ[x], OddQ[x] ,
PrimeQ[x] .

Zahlenkonversion:

N[x,n]

wandelt eine beliebige reelle Zahl x in eine Gleitpunktzahl mit n-stelliger Präzision um.

Rationalize[x,dx]

nähert die Zahl x mit der Genauigkeit dx durch eine rationale Zahl.
 
Vordefinierte spezielle Zahlen (beliebiger Genauigkeit): PI (für die Zahl ), E (für die Zahl e), INFINITY (für ) und I (für die imaginäre Einheit).
 
Einige wichtige Operatoren mit ihrer Kurzform:

 
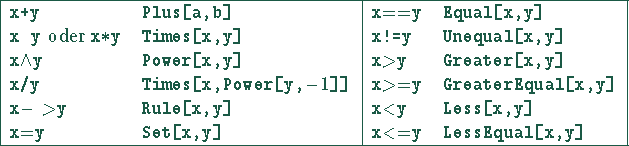
Set ist eine Zuweisung, bei der der Ausdruck auf der linken Seite durch den auf der rechten Seite dargestellt wird (einer Variablen wird beispielsweise eine Zahl zugewiesen).

Rule ist dagegen eine Transformationsregel, die oft mit dem Ersetzungsoperator als x/.yz bzw. Replace[x,yz] auftritt. Im Ausdruck x werden dabei alle Elemente y durch den Ausdruck z ersetzt.
 
Die rechte Seite wird bei diesen Zuweisungs- oder Transformationsoperatoren sofort ausgewertet.
 
Verzögert wirkende Operatoren, x:=y oder SetDelayed[x,y] und x:>y oder RuleDelayed[x,y] , Transformationen oder Zuweisungen, bei denen die rechte Seite erst bei Aufruf der linken ausgewertet wird.