|
|
|
|
|
|
|
|
Für selbstähnliche Strukturen, charakterisiert durch die Parameter
N und s gilt das Potenzgesetz
Hausdorff-Dimension, der Exponent D in diesem Skalierungsgesetz.
Für viele Objekte der klassischen Geometrie, wie Strecke, Quadrat
und Würfel stimmt die
Euklidische Dimension mit der Hausdorff-Dimension überein.
Strecke: 
Potenzgesetz: 
.
Hausdorff-Dimension: D=1.
Quadrat: 
Potenzgesetz: 
.
Hausdorff-Dimension: D=2.
Würfel: 
Potenzgesetz: 
.
Hausdorff-Dimension: D=3.
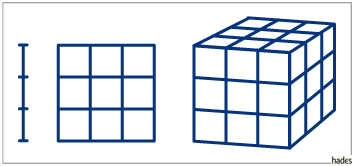
Die Hausdorff-Dimensionen von Strecke, Quadrat, Würfel, Dreieck
etc. sind unabhängig von N bzw. s! Teilt man beispielsweise
das Quadrat in 
um den Faktor 
verkleinerte Quadrate, so erhält man ebenfalls die
Hausdorff-Dimension 2.
Komplexe selbstähnliche Objekte besitzen i.a. eine
gebrochene Hausdorff-Dimension. Deshalb werden sie auch Fraktale
(engl. fraction = Bruch) genannt. Einige dieser Objekte sind die
Cantor-Menge, die Koch-Kurve und das Sierpinski-Dreieck.
|
|
|
|
|
|
|
|
