|
|
|
|
|
|
|
|
in eine Summe
von Brüchen. Zähler 
und Nenner 
sollen keine
gemeinsamen Polynomfaktoren haben und der Grad von 
(n),
soll kleiner als der Grad von 
(m), sein.
Die Produktdarstellung von 
ist:
wobei 
die k Nullstellen 
-ten Grades des Polynoms sind.
Der Restterm lasse sich als Produkt von irreduziblen (d.h. im Bereich der reellen Zahlen nicht in Linearfaktoren zerlegbaren) quadratischen Polynomen darstellen.
Zu jeder Nullstelle 
des Grades 
werden Terme bis zur
Potenz 
gebildet.
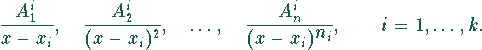
Ebenso werden Ausdrücke zu den Resttermen 
der Vielfachheit 
gebildet.
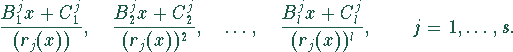
Alle diese Terme werden addiert:
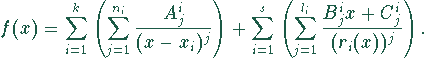
Meist ist es praktisch, zunächst die Gleichung mit dem Nennerpolynom
zu multiplizieren, um so eine Polynomgleichung zu erhalten.
Durch Koeffizientenvergleich können
die Koeffizienten der Partialbruchzerlegung gebildet werden.
Oft ist es jedoch einfacher, durch Einsetzen spezieller Werte (z.B.
, Nullstellen des Nennerpolynoms) jeweils alle Koeffizienten
bis auf einen zu eliminieren.
|
|
|
|
|
|
|
|
