|
|
|
|
|
|
|
|
streng monoton steigend für 
. 
ist sie konkav
(jeweils für 
). 
sieht die Kurve wie eine Hyperbel aus, ist konvex und
streng monoton fallend im Bereich 
.
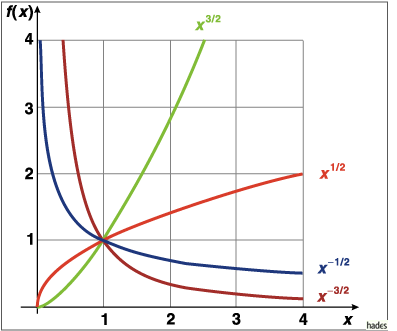
Mathematica Code:
Plot[{x^(1/2),x^(3/2),x^(-1/2),x^(-3/2)},{x,0,4}, PlotRange->{{0,4},{0,4}},
PlotStyle->{{Hue[0]},{Hue[0.3]},{Hue[0.6]},{Hue[0.8]}}, AspectRatio->Automatic]
Das Verhalten für 
ergibt sich aus m und n:
m und n ungerade: Die Funktion ist punktsymmetrisch zum
Ursprung. Der Graph 
senkrecht die x-Achse,
für m>n läuft er waagrecht ein.
m gerade und n ungerade: Die Funktion ist spiegelsymmetrisch zur
y-Achse. Für 
besitzt sie bei 
eine Knickstelle.
m ungerade und n gerade: die Funktion ist nicht für 
definiert.
Neilsche Parabel (semikubische
Parabel) mit 
, 
.
Das folgende Bild zeigt weitere Potenzfunktionen mit gebrochenen Exponenten:
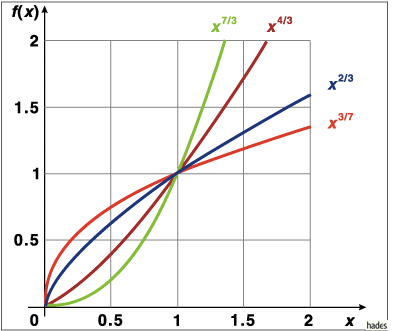
Mathematica Code:
f1=Plot[{x^(3/7),x^(7/3),x^(2/3),x^(4/3)},{x,0,2}, PlotRange->{{-2,2},{-2,2}},
PlotStyle->{{Hue[0]},{Hue[0.3]},{Hue[0.6]},{Hue[0.8]}}, AspectRatio->Automatic]
f2=Plot[{-Abs[x]^(3/7),-Abs[x]^(7/3),Abs[x]^(2/3),Abs[x]^(4/3)},{x,-2,0},
PlotRange->{{-2,2},{-2,2}}, PlotStyle->{{Hue[0]},{Hue[0.3]},{Hue[0.6]},{Hue[0.8]}},
AspectRatio->Automatic]
Show[{f1,f2}]
|
|
|
|
|
|
|
|
