|
|
|
|
|
|
|
|
, direkt
als (natürliche) Exponentialfunktion
darstellbar:
Selbstpotenzierende Funktion 
, analog auf die
Exponentialfunktion zurückführbar.
ist nur für 
definiert und läßt sich durch
stetig auf 
erweitern.
Die Funktion besitzt an der Stelle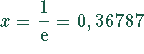 
ein
Minimum mit 
und steigt dann schneller als die
Exponentialfunktion gegen unendlich.
,
analog umformbar, besitzt ein Maximum bei 
und geht
für große Werte gegen 1.
Im folgenden Bild ist die selbstpotenzierende Funktion nebst ihrer Ableitung dargestellt.
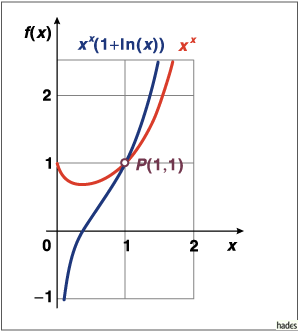
Mathematica Code:
Plot[{x^x,x^x (1+ Log[x])},{x,0.01,2.5},PlotRange->{{-0.5,2.5},{-1,2.5}},
PlotStyle->{{Hue[0]},{Hue[0.6]}},AspectRatio->Automatic]
Hyperbolische Funktionen 
,
darstellbar durch Summen, Differenzen und Quotienten von
Exponentialfunktionen.
Integralexponentialfunktion Ei(x), definiert durch das Integral
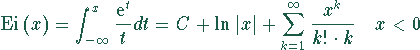
mit der Eulerschen Konstante 
.
Im folgenden Bild sind die Integralexponentialfunktion und die Integrallogarithmusfunktion dargestellt.
Mathematika Code:
f2=Plot[LogIntegral[x],{x,0,4},PlotRange->{{-3.3,4.3},{-2.2,4.2}},
PlotStyle->{Hue[0]},AspectRatio->Automatic]
f1=Plot[{ExpIntegralEi[x],ExpIntegralE[1,x]},{x,-3,4},
PlotRange->{{-3.3,4.3},{-2.2,4.2}},PlotStyle->{{Hue[0.3]},{Hue[0.6]}},
AspectRatio->Automatic]
Show[{f1,f2}]
Thetafunktionen , unendliche Summen von
Exponentialfunktionen mit Quadratzahlen
bzw.
den Quadraten von ungeraden Zahlen 
als Faktor
im Argument, z.B.:
Gaußfunktionen, Exponentialfunktionen mit quadratischem Argument
.
|
|
|
|
|
|
|
|
