|
|
|
|
|
|
|
|
besitzt ein Maximum bei 
und fällt schnell
gegen 0 ab. Mit größerem a (kleinerem 
) fällt die Kurve
schneller gegen 0. Die Fläche unter der Kurve wird kleiner.
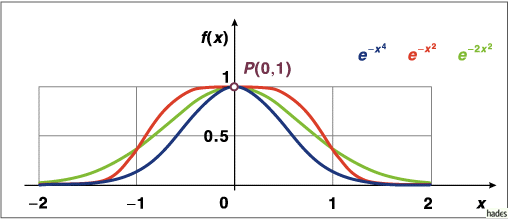
Mathematica Code:
Plot[{Exp[-x^2],Exp[-2x^2],Exp[-x^4]},{x,-2,2},PlotRange->{{-2.2,2.2},{-0.1,1.3}},
PlotStyle->{{Hue[0]},{Hue[0.3]},{Hue[0.6]}},AspectRatio->Automatic]
Wird die Fläche unter der Kurve konstant gehalten, so wird die Kurve schmaler und in der Mitte höher.
Die Funktionen 
mit n positiv und gerade zeigen
ähnliches Verhalten wie die Gaußkurve, allerdings mit schnellerem
Abfallverhalten. Die Asymptote ist 
.
Die Funktionen 
mit n positiv und
ungerade zeigen ein ähnliches Verhalten wie 
, jedoch
ebenfalls mit stärkerem Abfall.
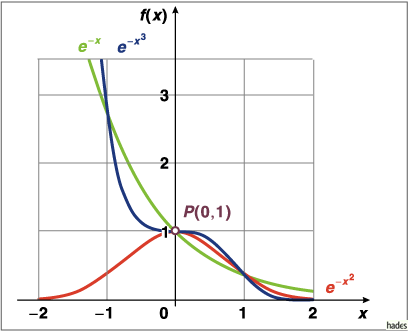
Mathematica Code:
Plot[{Exp[-x],Exp[-x^3],Exp[-x^2]},{x,-2,2},PlotRange->{{-2.2,2.2},{-0.1,3.5}},
PlotStyle->{{Hue[0]},{Hue[0.8]},{Hue[0.3]}},AspectRatio->Automatic]
Die Funktion 
hat bei 
eine
Definitionslücke, die rechtsseitig (
) durch den Punkt
halbstetig (von rechts) angeschlossen werden kann.
Von links divergiert die Funktion gegen 
. Für sehr große
positive 
und negative 
Werte von x geht
die Funktion gegen 1. Mit größerem a steigt die Funktion bei
negativen x stärker und bei positiven x schwächer an.
Die Funktionen 
mit n negativ und ungerade, haben ein
ähnliches Verhalten wie 
, allerdings mit
stärkerem Anstieg.
Eine bemerkenswerte Eigenschaft hat 
(und analog
, mit n gerade und negativ). Die Funktion läßt sich durch
den Punkt (
) stetig erweitern und ist dann überall (auch
am Punkt 
) beliebig oft differenzierbar.
Für sehr große (und sehr kleine) Werte geht die Funktion gegen 1.
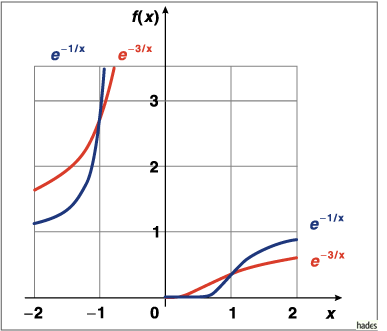
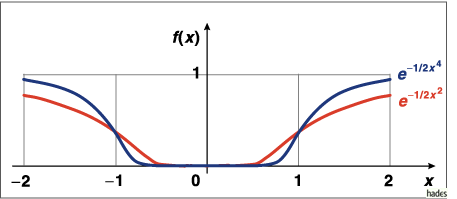
Mathematica Code:
f1=Plot[{Exp[-1/x],Exp[-1/x^3]},{x,0.01,2},PlotRange->{{-2.2,2.2},{-0.5,3.5}},
PlotStyle->{{Hue[0]},{Hue[0.13]},{Hue[0.3]}},AspectRatio->Automatic]
f2=Plot[{Exp[-1/x],Exp[-1/x^3]},{x,-2,-0.1},PlotRange->{{-2.2,2.2},{-0.5,3.5}},
PlotStyle->{{Hue[0.6]},{Hue[0.8]},{Hue[0.9]}},AspectRatio->Automatic]
Show[{f1,f2}]
f3=Plot[{Exp[-1/x^2],Exp[-1/x^4]},{x,0.01,2},PlotRange->{{-2.2,2.2},{-0.5,1.5}},
PlotStyle->{{Hue[0]},{Hue[0.8]},{Hue[0.3]}},AspectRatio->Automatic]
f4=Plot[{Exp[-1/x^2],Exp[-1/x^4]},{x,-2,-0.01},PlotRange->{{-2.2,2.2},{-0.5,1.5}},
PlotStyle->{{Hue[0]},{Hue[0.8]},{Hue[0.3]}},AspectRatio->Automatic]
Show[{f3,f4}]
|
|
|
|
|
|
|
|
