|
|
|
|
|
|
|
|
Lineare Unabhängigkeit in der Ebene, zwei Vektoren in
der Ebene,
sind linear unabhängig, wenn die Vektorgleichung
nur die triviale Lösung 
besitzt.
Diese Vektorgleichung ist gleichwertig dem linearen
Gleichungssystem in r und s:
Die Vektoren 
und 
sind
linear abhängig ( kollinear) bei Verschwinden der
Determinante, d.h., das lineare Gleichungssystem ist nicht eindeutig lösbar!
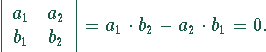
Lineare Abhängigkeit bedeutet, daß die zwei Geraden, auf denen
und 
liegen, parallel sind (sich nicht schneiden)
oder aufeinander liegen (unendlich viele Schnittpunkte haben). Dann
hat das obige lineare Gleichungssystem keine Lösung
Die Determinante ist Null!
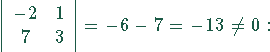
und 
sind linear unabhängig und
können als Basis verwendet werden.
Lösen des Gleichungssystems ergibt:
ist hier als ganzzahliges Vielfaches von
und 
darstellbar.
|
|
|
|
|
|
|
|
