|
|
|
|
|
|
|
|
derart, daß das
Ergebnis ein Skalar, also eine reelle Zahl, ist:
Die beiden Vektoren müssen gleich viele Komponenten haben!
Ist 
der zwischen den Vektoren eingeschlossene Winkel,
dann gilt:
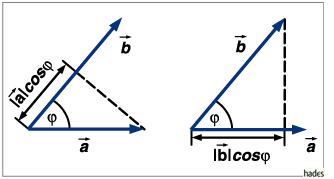
Anschauliche Bedeutung des Skalarproduktes:
Projektion von 
auf 
, multipliziert mit
oder
Projektion von 
auf 
, multipliziert mit
.
Komponentendarstellung, ,,Zeile mal Spalte``:
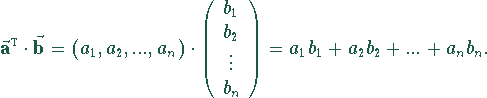
In Matrixschreibweise ist die Reihenfolge der Vektoren
extrem wichtig! 
ergibt einen Skalar
(Zeile mal Spalte), aber 
ergibt eine
Matrix (das dyadische Produkt).
|
|
|
|
|
|
|
|
