|
|
|
|
|
|
|
|
Geometrische Interpretation: Transformation der Koordinatenachsen auf die Symmetrieachsen der Flächen.
Eliminieren der gemischt-quadratischen Terme durch die Forderung, daß M diagonal ist:
mit den Eigenwerten 
und den Eigenvektoren
.
Berechnung der Eigenwerte 
aus:
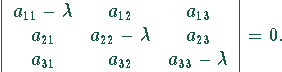
Bei doppelten (dreifachen) Eigenwerten können daraus zwei (drei)
beliebige aufeinander senkrecht stehende Achsen als Hauptachsen
gewählt werden.
Drehung der Koordinatenachsen auf die Richtung der Eigenvektoren
von 
ergibt folgende Gleichungsform:
mit
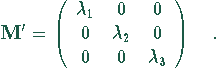
Eliminieren der linearen Terme durch folgende Verschiebung:
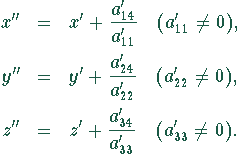
Endform nach Drehung und Verschiebung:
mit den Eigenwerten 
der Matrix 
.
|
|
|
|
|
|
|
|
