|
|
|
|
|
|
|
|
Länge, Zeit, Temperatur, Masse, Arbeit, Energie, Potential,
Kapazität.
Vektor, gerichtete Größe (Strecke), dargestellt durch einen Pfeil. Richtung des Pfeiles bestimmt die Richtung des Vektors. Länge des Pfeiles entspricht der Maßzahl.
Bezeichnung: Im allgemeinen mit lateinischen Buchstaben
im Fettdruck, versehen mit einem
Pfeil (
), auch üblich sind
deutsche Buchstaben
bzw. die Notationen (
etc.).
Eine eindeutige Festlegung erhält man
ebenfalls durch die Angabe von Anfangs- und Endpunkt, P und
Q: 
.
Geschwindigkeit, Beschleunigung, elektrische
und magnetische Feldstärke, Gravitationskraft, Ortsvektor,
Drehmoment.
Viele Vektoren sind - wie die meisten Rechenregeln -
anschaulich in zwei oder drei Dimensionen (Ebene, Raum)
gegeben, das Vektorkonzept läßt sich aber direkt auf n
Dimensionen ausdehnen. n-dimensionale Vektoren (auch mit n > 1000)
haben große praktische Bedeutung bei der Behandlung
großer linearer Gleichungssysteme.
Betrag oder Norm, Länge eines Vektors , Abstand des Anfangspunktes
vom Endpunkt, bestimmt die Länge des Vektors:
Durch die Angabe von Betrag und Richtung ist ein
Vektor 
eindeutig bestimmt.
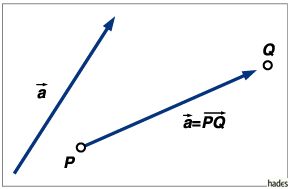
Relevant für die Bestimmung eines Vektors sind
nur Betrag und Richtung, nicht dagegen die
genaue Lage im Raum: Der ,,Vektor`` ist gewissermaßen ein
Symbol für alle Pfeile, die durch Parallelverschiebung
aus ihm hervorgehen können.
|
|
|
|
|
|
|
|
