






 |
 |
 |
 |
 |
 |
 |
 T: Verschiebung des Achsenvektors, so daß der Bezugspunkt
T: Verschiebung des Achsenvektors, so daß der Bezugspunkt
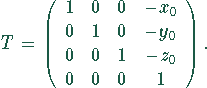

![]() : Rotation des Achsvektors um einen Winkel
: Rotation des Achsvektors um einen Winkel ![]() um
die x-Achse, so daß
um
die x-Achse, so daß ![]() , mit
, mit ![]() ,
in der
,
in der ![]() -Ebene liegt. Für
-Ebene liegt. Für ![]() muß gelten:
muß gelten:
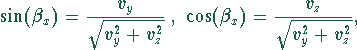
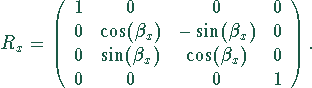

![]() : Rotation um die y-Achse, so daß der (gedrehte)
Rotationsachsenvektor mit der z-Achse zusammenfällt. Dies
erfordert die Drehung um den Winkel
: Rotation um die y-Achse, so daß der (gedrehte)
Rotationsachsenvektor mit der z-Achse zusammenfällt. Dies
erfordert die Drehung um den Winkel ![]() mit
mit
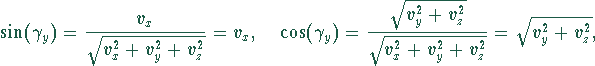
![]()
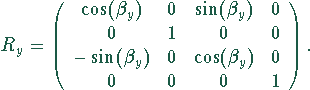

![]() : Die Rotation um den vorgegebenen Drehwinkel
: Die Rotation um den vorgegebenen Drehwinkel ![]() um die Rotationsachse erfolgt jetzt um die z-Achse:
um die Rotationsachse erfolgt jetzt um die z-Achse:
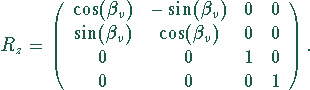
 Umkehrung: Die schrittweise Transformation der Rotationsachse in die
z-Achse wird durch Anwendung der inversen Transformation in
umgekehrter Reihenfolge rückgängig gemacht, wobei
Umkehrung: Die schrittweise Transformation der Rotationsachse in die
z-Achse wird durch Anwendung der inversen Transformation in
umgekehrter Reihenfolge rückgängig gemacht, wobei
![]()
und ![]() durch Einsetzen des negativen Translationsvektors
entsteht.
durch Einsetzen des negativen Translationsvektors
entsteht.
 Allgemeine Rotationsmatrix
R für eine
Drehung von Objekten um eine beliebige Rotationsachse im Raum wird erreicht
durch Multiplikation dieser sieben Matrizen:
Allgemeine Rotationsmatrix
R für eine
Drehung von Objekten um eine beliebige Rotationsachse im Raum wird erreicht
durch Multiplikation dieser sieben Matrizen:
![]()
 |
 |
 |
 |
 |
 |
 |
