|
|
|
|
|
|
|
|
:
Orthogonale Parallelprojektion
auf die 
-Ebene:
, 
, 
.
Zentralprojektion auf eine zur 
-Ebene parallele Ebene,
Projektionszentrum im Ursprung:
, 
.
Zentralprojektion auf die 
-Ebene, Projektionszentrum auf
der negativen z-Achse:
, 
, 
Die Zentralprojektion 
definiert im Fall 
eine sogenannte
Ein-Punkt-Perspektive: Parallele Geraden,
die nicht parallel zur Projektionsebene liegen, konvergieren bei der
Projektion in einem Punkt. Der Schnittpunkt der Parallelen zur
z-Achse heißt Fluchtpunkt.
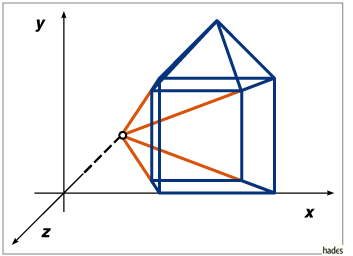
Im dreidimensionalen Raum schneiden
sich parallele Geraden nur im Unendlichen. Der Fluchtpunkt
kann deshalb als Projektion eines unendlich
fernen Punktes der z-Achse aufgefaßt werden mit homogenen Koordinaten
.
Multiplikation mit 
und anschließender Division durch die homogene
Koordinate w ergibt die Fluchtpunktkoordinaten:
Ist ein gewünschter Fluchtpunkt (
vorgegeben und
der Abstand q zum Projektionszentrum bekannt, dann ist wegen
der Richtungsvektor
und damit die Projektionsmatrix eindeutig definiert.
Steht die Projektionsebene nicht mehr senkrecht auf der
z-Achse, sondern liegt beliebig im Raum, dann gibt es bis zu drei
Fluchtpunkte. Die Projektionen werden entsprechend
Ein-Punkt-, Zwei-Punkt- oder Drei-Punkt-Perspektive genannt:
Zwei-Punkt-Perspektive: Die Projektionsebene schneidet zwei Hauptachsen. Die Parallelen zu diesen Hauptachsen schneiden sich in zwei Fluchtpunkten.
Drei-Punkt-Perspektive: Die Projektionsebene schneidet drei Hauptachsen. Es entstehen drei Fluchtpunkte.
|
|
|
|
|
|
|
|
