Koordinatentransformation
Die Koordinatentransformation erfolgt dadurch, daß eine Nebenbedingung
( Pivot-Zeile) zunächst nach einer Nichtbasisvariablen
( Pivot-Spalte)
aufgelöst wird. Diese wird damit zur Basisvariablen. Mittels der
aufgelösten Gleichung wird dann die Variable,
nach der aufgelöst wurde, in allen anderen Gleichungen substituiert.
Die Basisvariable, die ursprünglich zur Pivot-Zeile gehörte, wird dann
in der Pivot-Spalte angeordnet und wird damit zur Nichtbasisvariablen.
Somit hat ein Austausch zwischen der
ursprünglichen Basisvariablen der Pivot-Zeile und der ursprünglichen
Nichtbasisvariablen der Pivot-Spalte stattgefunden.
Der Koeffizient im Kreuzungspunkt von Pivot-Zeile und Pivot-Spalte
heißt Pivot-Element (engl.: pivot = Drehpunkt).
Als Pivot-Spalte jp kann jeweils die Spalte mit dem größten positiven
Koeffizienten der Zielfunktion gewählt werden:
Als Pivot-Zeile ip soll die Zeile gewählt werden, die den betragsmäßig
kleinsten Quotienten des Wertes der rechten Spalte und des gleichzeiligen
negativen Koeffizienten der Pivot-Spalte enthält:
Hierdurch ist gewährleistet, daß immer zu Eckpunkten fortgeschritten wird,
in deren Richtung die Zielfunktion am stärksten ansteigt.
Die Umrechnung des Tableaus ( Koordinatentransformation)
läßt sich dann wie folgt schematisieren.
- Im neuen Tableau sind die Variablen von Pivot-Spalte und Pivot-
Zeile vertauscht.
- An Stelle des Pivot-Elements tritt sein Reziprokwert.
- Die restlichen Koeffizienten der Pivot-Spalte werden durch das
Pivot-Element dividiert.
- Die übrigen Elemente der Pivot-Zeile werden durch das Pivot-Element
dividiert und dann mit
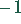multipliziert.
- Zu allen anderen Koeffizienten des Tableaus (inklusive jenen der
Zielfunktion) wird das Produkt des gleichzeiligen Koeffizienten
der Pivot-Spalte - vor der Umrechnung - und des gleichspaltigen
Koeffizienten der Pivot-Zeile - nach der Umrechnung - addiert.
Die Nichtnegativitätsbedingungen werden beim Simplexalgorithmus
automatisch berücksichtigt. Die einzelnen Transformationen werden als
Iterationen bezeichnet.
