|
|
|
|
|
|
|
|
Addition und Subtraktion von Tensoren gleicher Stufe, analog zu Vektoren und
Matrizen werden Tensoren gleicher Stufe komponentenweise addiert und subtrahiert:
Multiplikation eines Tensors mit einem Skalar, erfolgt ebenfalls
komponentenweise.
Multiplikation zweier Tensoren, das Produkt 
eines
Tensors n-ter Stufe 
und eines Tensors r-ter Stufe 
ist ein
Tensor 
-ter Stufe mit den Komponenten
Es gelten Distributiv- und Assoziativgesetz:
Verjüngung eines Tensors, in einem Tensor n-ter Stufe 
werden zwei
Indizes gleichgesetzt, dann wird über sie summiert. Es entsteht ein Tensor 
-ter Stufe.
Überschieben von Tensoren, zwei Tensoren werden miteinander
multipliziert und dann verjüngt.
Die Verjüngung des dyadischen Produkts (Tensor 2. Stufe) zweier
Vektoren 
und 
führt auf das Skalarprodukt 
. Das Ergebnis ist ein Tensor 0. Stufe.
ein Tensor 2. Stufe.
Verjüngung: 
, Summation über j
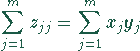
Tensor 0. Stufe.
Das Überschieben von zwei Tensoren 2. Stufe (Matrizen) A und B führt auf die
Matrixmultiplikation 
.
Tensormultiplikation:
Tensor 4. Stufe
Verjüngung: 
. Summation über l.
Tensor 2. Stufe.
|
|
|
|
|
|
|
|
