






 |
 |
 |
 |
 |
 |
 |
Lineare Koordinatentransformation:
![]()
Transformation der Tensorkomponenten:
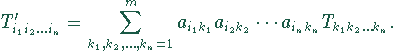
 Ein Tensor n-ter Stufe auf einem dreidimensionalen Vektorraum besitzt
Ein Tensor n-ter Stufe auf einem dreidimensionalen Vektorraum besitzt ![]() Komponenten.
Komponenten.
Tensor 0. Stufe , einkomponentige Größe, die in allen
Koordinatensystemen den gleichen Wert hat. Ein Tensor 0. Stufe ist ein invarianter
Skalar.
Tensor 1. Stufe , m-komponentige Größe, die sich wie ein Vektor transformiert. Ein Tensor 1. Stufe kann als Vektor dargestellt werden.
![]()
Tensor 2. Stufe , ![]() -komponentige Größe, die als
-komponentige Größe, die als ![]() Matrix dargestellt werden kann:
Matrix dargestellt werden kann:
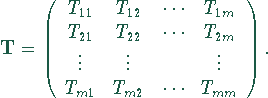
 Die Darstellung eines Vektors v (z.B. des Geschwindigkeitsvektors) im
Die Darstellung eines Vektors v (z.B. des Geschwindigkeitsvektors) im ![]() in
verschiedenen Basissystemen
in
verschiedenen Basissystemen ![]() ,
, ![]()
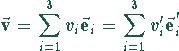
ändert nichts an seinem eigentlichen Wert. Man nennt ![]() eine invariante Größe.
eine invariante Größe.
Physikalische Gesetzmäßigkeiten, die als Gleichungen zwischen Tensoren geschrieben werden
können, ändern ihre mathematische Form beim Übergang in ein anderes Koordinatensystem nicht.
Symmetrischer Tensor, 2. Stufe,
![]() für alle
für alle ![]() .
.
Antisymmetrischer Tensor oder schiefsymmetrischer Tensor
2. Stufe,
![]() für alle
für alle ![]() .
.
 Die Diagonalelemente eines schiefsymmetrischen Tensors 2. Stufe sind Null,
Die Diagonalelemente eines schiefsymmetrischen Tensors 2. Stufe sind Null, ![]() .
.
Spur eines Tensors 2. Stufe, Summe der Diagonalelemente,
![]()
 Die Spur ist eine Tensorinvariante, sie bleibt bei linearen Koordinatentransfomationen
erhalten:
Die Spur ist eine Tensorinvariante, sie bleibt bei linearen Koordinatentransfomationen
erhalten:
![]()
 Trägheitstensor in der Mechanik, symmetrischer
Tensor 2. Stufe, mit dessen Hilfe der Drehimpuls eines starren Körpers bezüglich einer
beliebigen Rotationsachse berechnet werden kann.
Trägheitstensor in der Mechanik, symmetrischer
Tensor 2. Stufe, mit dessen Hilfe der Drehimpuls eines starren Körpers bezüglich einer
beliebigen Rotationsachse berechnet werden kann.
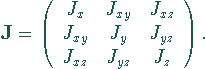
![]() : Trägheitsmomente bezüglich der Koordinatenachsen.
: Trägheitsmomente bezüglich der Koordinatenachsen.
![]() : Deviationsmomente bezüglich der Koordinatenachsen.
: Deviationsmomente bezüglich der Koordinatenachsen.
 Die Deviationsmomente verschwinden im Hauptachsensystem.
Die Deviationsmomente verschwinden im Hauptachsensystem.
 Drucktensor in der Hydromechanik, Spannungstensor in der
Elastomechanik, Feldstärketensor in der Elektrodynamik.
Drucktensor in der Hydromechanik, Spannungstensor in der
Elastomechanik, Feldstärketensor in der Elektrodynamik.
 |
 |
 |
 |
 |
 |
 |
