|
|
|
|
|
|
|
|
Laplace-Entwicklung nach einer Zeile oder Spalte mit möglichst
vielen Nullen.
Durch elementare Umformungen wird der Wert der
Determinante nicht geändert.
Nullen in Zeilen erzeugen durch Addition (Subtraktion) von
Vielfachen von Zeilen.
Nullen in Spalten erzeugen durch Addition (Subtraktion) von
Vielfachen von Spalten.
Berechnung von n-reihigen Determinanten
durch elementare Umformungen: Die praktische
Berechnung von Determinanten höherer Ordnung erfolgt mit
numerischen Verfahren. Die Matrix wird dabei durch
elementare Umformungen, die den Wert der Determinante nicht
verändern, in eine Dreiecksmatrix übergeführt. Die
Determinante ist dann einfach zu berechnen:
Die Determinante
einer Dreiecksmatrix ist das Produkt der Elemente auf
der Hauptdiagonalen:
für
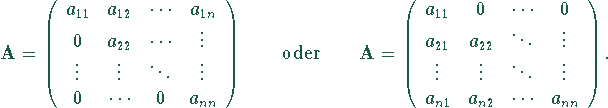
Entwickeln nach der ersten Spalte:
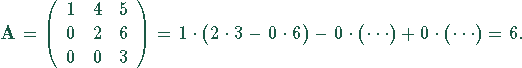
Solche Verfahren zur Matrixumformung werden zur Lösung linearer
Gleichungssysteme herangezogen.
|
|
|
|
|
|
|
|
