Hauptsatz der Integralrechnung
 Hauptsatz der Differential- und Integralrechnung,
ist
Hauptsatz der Differential- und Integralrechnung,
ist  eine Stammfunktion von
eine Stammfunktion von 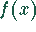 , also
, also
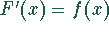 , so gilt:
, so gilt:
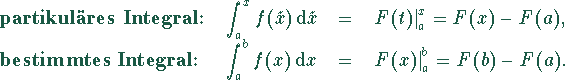
Berechnung eines bestimmten Integrales:
Man integriert eine Funktion  (den Integranden), indem man
(den Integranden), indem man
- eine Stammfunktion
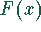 sucht,
deren Ableitung wieder die Ursprungsfunktion ergibt,
sucht,
deren Ableitung wieder die Ursprungsfunktion ergibt,
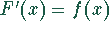 ,
,
- den Funktionswert der Stammfunktion
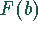 an der oberen Grenze b berechnet und dann
an der oberen Grenze b berechnet und dann
- den Stammfunktionswert
 an der
unteren Grenze a abzieht.
an der
unteren Grenze a abzieht.
- Die Integrationskonstante fällt beim Integrieren heraus


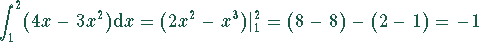
 Das Partikulärintegral ist eine Funktion von x,
während das bestimmte Integral
eine bestimmte feste Zahl liefert.
Das Partikulärintegral ist eine Funktion von x,
während das bestimmte Integral
eine bestimmte feste Zahl liefert.















 Hauptsatz der Differential- und Integralrechnung,
ist
Hauptsatz der Differential- und Integralrechnung,
ist 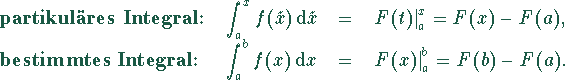
![]() (den Integranden), indem man
(den Integranden), indem man
![]()

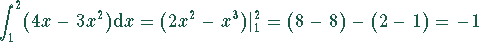
 Das Partikulärintegral ist eine Funktion von x,
während das bestimmte Integral
eine bestimmte feste Zahl liefert.
Das Partikulärintegral ist eine Funktion von x,
während das bestimmte Integral
eine bestimmte feste Zahl liefert.






