|
|
|
|
|
|
|
|
Symbolisch:
Integrationaufgabe wird durch
zwei Teilintegrationen gelöst:
Anwendung der Regel besonders bei Produkten von Funktionen
als Integrand.
Die Ableitung 
sollte eine einfachere Funktion ergeben als 
.
Die Funktion 
sollte einfach zu integrieren
und das Ergebnis sollte nicht komplizierter sein.
Gegebenfalls die partielle Integration mehrfach
hintereinander anwenden.
.
Manchmal führt die Einführung eines Produktes zum Ziel.
.
Merkregel:
1) Integriere den ersten Faktor,
2) schreibe das entstehende Produkt hin,
3) leite dann den zweiten Faktor ab und
4) schreibe das entstehende Produkt mit einem Minuszeichen unter das
Integral.
Häufig wird das Minuszeichen vor dem Integral vergessen,
besonders bei mehrfacher Anwendung der partiellen
Integration.
Manchmal erhält man das Ausgangsintegral bei der partiellen
Integration wieder. Dann löst man
die Gleichung nach diesem Integral auf.
.
|
|
|
|
|
|
|
|
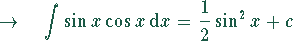