Spezialfälle der partiellen Integration
a) Integrand ist Produkt aus einem Polynom 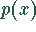 vom Grade n und einer der
Funktionen
vom Grade n und einer der
Funktionen 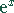 ,
,  ,
, 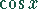 ,
, 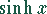 ,
, 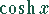 :
:
Mehrfache (n-fache) partielle Integration für 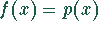 .
.

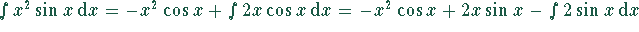
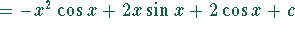 .
.
b) Integrand ist Produkt aus zwei der Funktionen
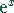 ,
,  ,
, 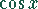 ,
, 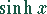 ,
, 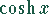 :
:
Zweimalige Produktintegration führt auf Ausgangsintegral zurück,
nach dem dann die Gleichung aufgelöst wird.
Gegebenenfalls folgende Beziehungen verwenden:
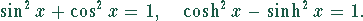

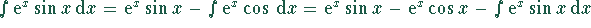
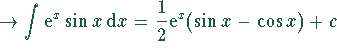 .
.
 Bei einem Produkt aus
Bei einem Produkt aus 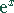 mit einer Hyperbelfunktion
diese durch
mit einer Hyperbelfunktion
diese durch
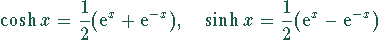
ersetzen und mit 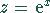 substituieren.
substituieren.
c) Integrand ist Produkt aus einer rationalen Funktion und einer
logarithmischen, Arkus- oder Area-Funktion:
Man setze die rationale Funktion gleich 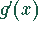 .
.

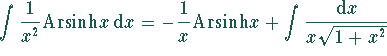
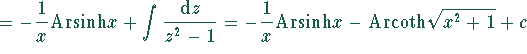 ,
,
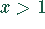 .
.
(Substitution 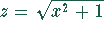 ).
).

















![]()

![]()
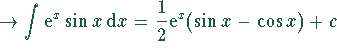 .
.
 Bei einem Produkt aus
Bei einem Produkt aus ![]() mit einer Hyperbelfunktion
diese durch
mit einer Hyperbelfunktion
diese durch
![]()
![]() substituieren.
substituieren.
![]() .
.

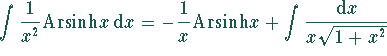
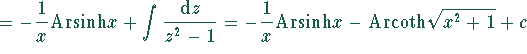 ,
,
![]() .
.![]() ).
).






