Anwendungen des Mittelwertsatzes
Numerische Integration
mit Gauß-Verfahren n-ter Ordnung,
die Funktionswerte werden nicht
am Rand des Intervalles  , sondern an geeigneten
x-Werten im Innern von
, sondern an geeigneten
x-Werten im Innern von  berechnet, so daß das Integral
bis zu einem Polynom n-ter Ordnung exakt ist.
berechnet, so daß das Integral
bis zu einem Polynom n-ter Ordnung exakt ist.
 Erweiterter erster Mittelwertsatz der Integralrechnung:
sind
Erweiterter erster Mittelwertsatz der Integralrechnung:
sind  und
und 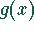 im Intervall
im Intervall 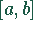 stetig und
wechselt
stetig und
wechselt 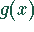 im Intervall das Vorzeichen nicht, so gilt
im Intervall das Vorzeichen nicht, so gilt

 Erweiterter zweiter Mittelwertsatz der Integralrechnung,
ist
Erweiterter zweiter Mittelwertsatz der Integralrechnung,
ist  monoton und beschränkt und ist
monoton und beschränkt und ist  im Intervall
im Intervall  integrierbar, so gilt
integrierbar, so gilt
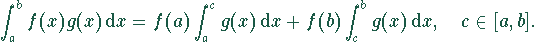















 Erweiterter erster Mittelwertsatz der Integralrechnung:
sind
Erweiterter erster Mittelwertsatz der Integralrechnung:
sind ![]()
 Erweiterter zweiter Mittelwertsatz der Integralrechnung,
ist
Erweiterter zweiter Mittelwertsatz der Integralrechnung,
ist ![]() monoton und beschränkt und ist
monoton und beschränkt und ist ![]() im Intervall
im Intervall ![]() integrierbar, so gilt
integrierbar, so gilt
![]()







