|
|
|
|
|
|
|
|
Satz von Rolle:
Wenn eine Funktion 
differenzierbar,
stetig und wenn
ist,
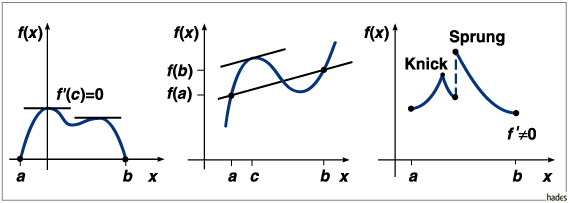
links Satz von Rolle, Mitte Mittelwertsatz
rechts Gegenbeispiel.
Zwischen zwei Nullstellen einer
differenzierbaren Funktion
liegt mindestens ein Extremum,
außer bei der konstanten Funktion 
.
Bei Sprungstellen oder Knicken
in 
gilt der Satz von Rolle nicht, da die
Differenzierbarkeitsvoraussetzung verletzt ist.
Die Funktion muß in den Randpunkten a und b stetig
sein.
Die Funktion kann bei
a und b noch weitere, absolute Extrema besitzen.
|
|
|
|
|
|
|
|
