|
|
|
|
|
|
|
|
Mittelwertsatz der Differentialrechnung
(Satz von Lagrange):
Wenn eine Funktion 
differenzierbar,
stetig ist,
Geometrische Deutung: Im Intervall 
existiert ein Punkt
,
in dem die Steigung der Tangente gleich der
Steigung der Sekante
durch 
und 
ist. Dies ist die mittlere Steigung.
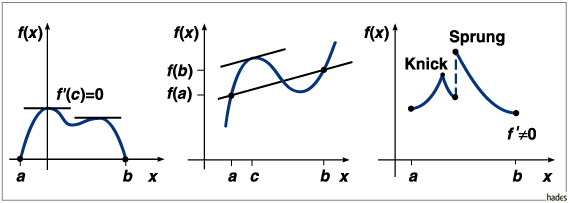
links Satz von Rolle, Mitte Mittelwertsatz
rechts Gegenbeispiel.
Die Bezeichnung Mittelwertsatz ist irreführend, es
müßte besser ,,Zwischenwertsatz`` heißen, da c nur
zwischen a und b liegt und nicht in der Mitte des
Intervalles.
Ein Fahrzeug fährt von Punkt A zu Punkt B mit einer
mittleren Geschwindigkeit von 80 km/h.
An mindestens einem Punkt C zwischen A und B muß
die momentane Geschwindigkeit mit der mittleren Geschwindigkeit
übereinstimmen.
Mittelwertsatz ist das Fundament der numerischen Differentiation.
Für 
folgt aus dem Mittelwertsatz der Satz von Rolle.
|
|
|
|
|
|
|
|
