|
|
|
|
|
|
|
|
Am Wendepunkt ändert sich das Vorzeichen der Krümmung.
Am Wendepunkt 
muß die zweite Ableitung
von 
Null sein (notwendige Bedingung),
Die Bedingung ist nicht hinreichend, d.h. es liegt nicht notwendigerweise
ein Wendepunkt vor.
, 
, 
, aber die
Funktion besitzt keinen Wendepunkt, sondern ein Minimum bei 
.
Notwendige und hinreichende Bedingung für einen Wendepunkt:
Wendepunkte mit senkrechter Tangente erfüllen diese Bedingungen i.a.
nicht, z.B. 
.
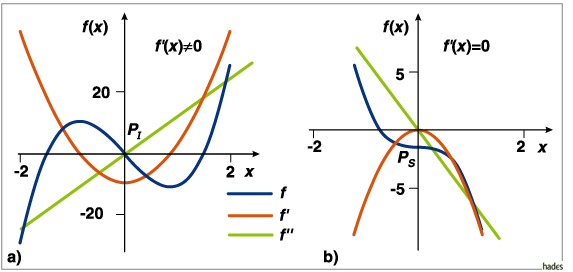
Wendepunkt und Sattelpunkt
Sattelpunkt (auch Stufen- oder Terassenpunkt),
spezieller Wendepunkt
mit waagrecht verlaufender Tangente:
Eine n-fach differenzierbare Funktion besitzt an einem
Punkt 
mit
folgendes Verhalten:
, 
,
,
d.h., bei 
liegt ein Minimum vor.
|
|
|
|
|
|
|
|
