|
|
|
|
|
|
|
|
Das Kurvenintegral existiert immer
für glatte Kurven C und auf C stetigen Funktionen f.
Das komplexe Kurvenintegral hängt mit den reellen
Kurvenintegralen mittels der Zerlegung 
zusammen:
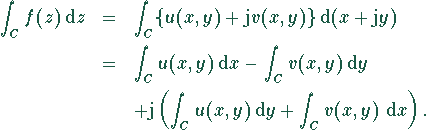
Die bekannten Eigenschaften reeller Kurvenintegrale übertragen sich:
Linearität:
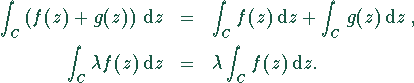
Umkehren der Integrationsrichtung:
(
bedeutet, daß die Kurve C im umgekehrten Sinn
durchlaufen wird).
Aufteilen in Teilintegrale:
Wenn a < c < b,
,
, dann ist
|
|
|
|
|
|
|
|
