|
|
|
|
|
|
|
|
einer Funktion 
: 
und eine Kurve 
mit
beliebigem, aber fest gewähltem Anfangspunkt 
, und
mit dem Endpunkt 
. 
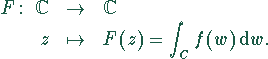
Das Integral ist wegunabhängig, da f analytisch ist. Der Wert des Integrals hängt jedoch noch vom Anfangspunkt a ab.
Unbestimmtes Integral der Funktion f,
die Gesamtheit aller Stammfunktionen (für alle a).
Die Integrationsregeln für die unbestimmte Integration
der elementaren komplexen Funktionen entsprechen denen im Reellen.
|
|
|
|
|
|
|
|
