|
|
|
|
|
|
|
|
Sei G ein einfach zusammenhängendes Gebiet,
b der Mittelpunkt des Kreises
, a ein Punkt innerhalb des Kreises.
Für 
gilt die Reihenentwicklung (geometrische Reihe)
da 
.
Sei f eine auf G analytische Funktion. Substitution der Reihenentwicklung in die erste Cauchysche Integralformel für f,
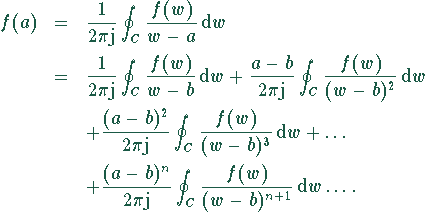
Komplexe Taylorreihe, Entwicklung der Funktion f um den Punkt b, folgt mit Hilfe der Cauchyschen Integralformeln aus der obigen Gleichung,
Die Entwicklung gilt
für alle Punkte a innerhalb des Kreises C.
|
|
|
|
|
|
|
|
