|
|
|
|
|
|
|
|
, 
der
zugehörigen homogenen linearen Differentialgleichung, so kann man
eine spezielle Lösung
der inhomogenen Differentialgleichung daraus berechnen.
Sind 
, 
linear unabhängige Lösungen der
Differentialgleichung
so ist eine Lösung 
der inhomogenen Differentialgleichung
gegeben durch
wobei
die Wronski-Determinante der Funktionen 
, 
ist.
Da 
und 
nach Voraussetzung linear unabhängig
sind, ist im gesamten Intervall 
Aus dem obigen Beispiel folgt: 
, 
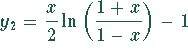. Somit
|
|
|
|
|
|
|
|
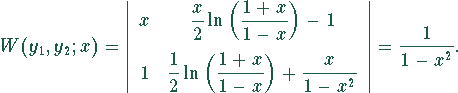
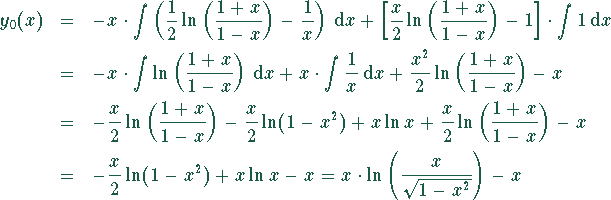
