|
|
|
|
|
|
|
|
Ordnung,
die Ordnung der höchsten auftretenden
Ableitungen von y.
Grad,
die höchste auftretende Potenz von y oder einer
seiner Ableitungen.
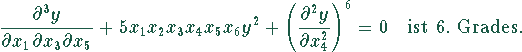
Lineare partielle Differentialgleichung, partielle
Differentialgleichung 1. Grades.
Homogene partielle Differentialgleichung,
falls kein (von y oder seinen Ableitungen) freies Glied auftritt.
Die Laplacegleichung für den ladungsfreien Raum
ist homogen (und linear).
Inhomogene DGl, falls von y und seinen Ableitungen freie
Glieder auftreten.
Die Poissongleichung für eine gegebene Ladungsverteilung ist
inhomogen:
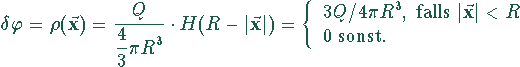
(homogen geladene Kugel vom Radius R, H ist die Sprungfunktion).
Integrationskonstante,
an die Stelle der
Integrationskonstanten treten im Falle der partiellen Differentialgleichungen freie
Funktionen der unabhängigen Veränderlichen.
Wellengleichung für schwingende Systeme in der Technischen
Mechanik und für elektromagnetische Wellen
Allgemeine Lösung:
Der Fall 
, d.h. 
mit 
ist erlaubt!
Lösung:
und 
sind erlaubt!
|
|
|
|
|
|
|
|
