|
|
|
|
|
|
|
|
sind skalare
Funktionen, 
ist das Integrationsvolumen und 
die
Oberfläche des Volumens.Erste Greensche Formel: Es wird gemäß der Produktregel
partiell integriert und der Gaußsche Integralsatz angewandt.
wobei 
der auf der Außenfläche stehende Normalenvektor ist.
Zweite Greensche Formel: Zweimalige Verwendung der ersten Greenschen Formel mit vertauschten Argumenten.
Die Bedeutung der Greenschen Formeln liegt in ihrem Nutzen bei der analytischen Lösung von Potentialgleichungen unter speziellen Randbedingungen.
Quellen von Potentialfeldern. Der Laplace-Operator verknüpft die Quellenstärke des Gradientenfeldes mit dem Potentialfeld.
Laplace-Gleichung
gilt im quellenfreien Raum.
.
Poisson-Gleichung gilt
bei Vorhandensein von Quellen
, wobei 
die Quellendichte ist.
Beide Gleichungen werden als Feldgleichungen zur Bestimmung des Potentialfeldes U (unter bestimmten Randbedingungen) verwendet.
Sie haben ihre Bedeutung vor allem in der Elektrostatik und
Elektrodynamik.
Das Fernfeld des Dipols 
erfüllt die Laplace-Gleichung:
|
|
|
|
|
|
|
|
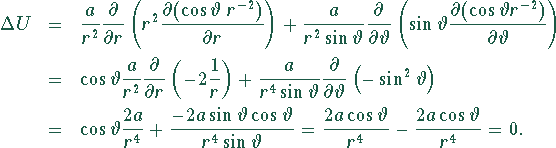
