|
|
|
|
|
|
|
|
Finite Elemente,
der Definitionsbereich der gesuchten
Funktion wird in kleine Bereiche aufgeteilt, auf denen die gesuchte
Funktion geeignet approximiert wird (z.B. durch Polynome).
Die im letzten Abschnitt erläuterte Methode der finiten
Differenzen war auf einem quadratischen Gitter definiert worden. Es
ist schwierig, sie für ein unregelmäßiges Gitter zu verwenden. Gerade
in der Technik ist es aber wichtig, das Gitter dort möglichst dicht
zu wählen, wo die Funktion sich stark ändert (wo sie sich nur wenig
ändert, sollte das Gitter nicht so dicht sein, um Speicherplatz zu
sparen und die Rundungsfehler klein zu halten). Außerdem möchte man
während der Berechnung das Gitter anpassen können. Das ist mit der
Methode der finiten Elemente viel besser möglich.
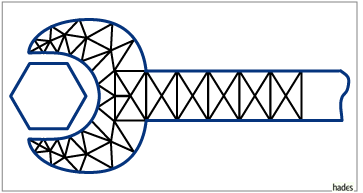
Beispiel für eine Zerlegung eines Objekts in finite Elemente
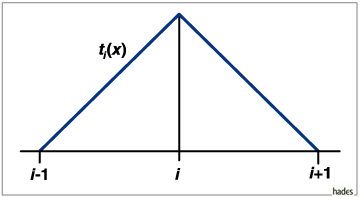
Beispiel einer Testfunktion im Element i.
|
|
|
|
|
|
|
|
