|
|
|
|
|
|
|
|
Notation: Für 
schreibt man auch 
und
für 
.
Die Funktion 
nennt man die
Fourier-Transformierte ( Spektralfunktion) von
und den Übergang
von 
nach 
Fourier-Transformation (Operator F).
Die Fourier-Transformation bildet den Zeitbereich auf den
Spektralbereich ab, indem der Funktion 
im Zeitbereich die
Funktion 
im Spektralbereich zugeordnet wird.
Wegen der Symmetrie von
und 
wird der Übergang von 
nach 
inverse Fourier-Transformation (Operator 
) genannt.
Auch hier gibt es verschiedene Konventionen, den
Faktor 
aufzuteilen:
a) Ein Faktor 
steht
sowohl vor dem Integral von 
als auch vor dem von 
.
b) Der Faktor 
steht nur vor dem Integral von
.
c) Der Faktor 
steht nur vor dem Integral von 
.
Hier wird die Konvention c) benutzt.
Kontinuierliches Amplitudenspektrum, entspricht dem
Amplitudenspektrum bei den Fourier-Reihen:
Kontinuierliches Phasenspektrum, entspricht dem Phasenspektrum bei den Fourier-Reihen:
Fouriercosinustransformation
(Cosinustransformation), bei geraden Funktionen 
gilt die
Relation
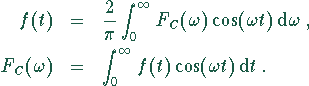
Fouriersinustransformation
(Sinustransformation), Entwicklung
nach Sinusfunktionen, die bei ungeraden Funktionen 
benutzt wird:
|
|
|
|
|
|
|
|
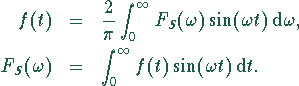
