|
|
|
|
|
|
|
|
eine
orthonormale Basis bildet.
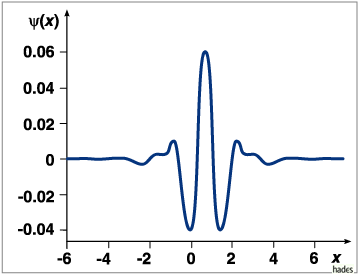
Battle-Lemarié-Wavelet, ein orthogonales Wavelet
Kompakter Träger , die Eigenschaft eines Wavelets, nur auf einem Teil
der Zeitachse von Null verschieden zu sein.
Die Haar-Funktion ist das einfachste Beispiel für ein orthogonales Wavelet
mit kompaktem Träger. Damit ist sie auch selbstdual, so daß die
Rekonstruktion mit den gleichen Basisfunktionen erfolgen kann.
Andere orthogonale Wavelets mit kompaktem Träger: Konstruktion nach
I. Daubechies (1988).
Daubechies-Wavelets orthogonale Wavelets mit kompakten Träger. Irreguläre Funktionen ohne geschlossene Darstellung, aber mit besonders guten numerischen Eigenschaften.
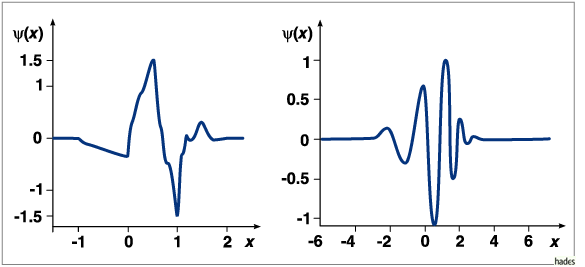
Daubechies-Wavelets der Typen 
und 
|
|
|
|
|
|
|
|
