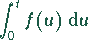|
|
|
|
|
|
|
|
, ist gleich der Bildfunktion 
der Originalfunktion 
, multipliziert mit 
:
Für eine Konstante gilt die Korrespondenz (s.o.):
Mit Hilfe des Integrationssatzes läßt sich damit die
Laplace-Transformierte der Funktion 
bestimmen, weil diese
als Integral über 
gegeben ist:
Der Integrationssatz liefert daher:
Im Originalbereich heben sich Differentiation und Integration
auf:
Dasselbe ist auch im Bildbereich der Fall:
|
|
|
|
|
|
|
|
