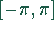|
|
|
|
|
|
|
|
wird damit aufgehoben. Durch
Einführung der Kreisfrequenz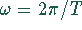 
(T: Periodendauer)
und durch die Substitution 
in den Koeffizienten und
der Fourier-Reihe erhält man die Form der Fourier-Reihe, die gültig ist für
Funktionen mit der Periodendauer T:
und den Koeffizienten:
und
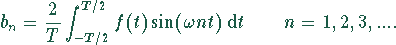
Die Teilschwingung in der Reihenentwicklung mit der kleinsten Kreisfrequenz
bezeichnet man als Grundschwingung,
alle übrigen Schwingungen mit den Vielfachen von 
nennt man Oberschwingungen.
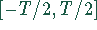auch das Intervall 
genommen
werden. Die Integrationsgrenzen laufen dann von 
bis T.
erhält dann
die Interpretation des doppelten Gleichstromanteils
( Gleichspannungsanteils) in der Entwicklung.
). Dann nimmt die Kreisfrequenz
die Rolle der Wellenzahl an (
), und die Periodendauer
T geht in die Wellenlänge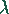 
über. Damit gilt für die
Wellenzahl 
.
|
|
|
|
|
|
|
|
