






 |
 |
 |
 |
 |
 |
 |
![]()
mit der dreifachen Nullstelle ![]() . Die
Partialbruchzerlegung dieses Ausdrucks lautet:
. Die
Partialbruchzerlegung dieses Ausdrucks lautet:
![]()
Zur Bestimmung von ![]() und
und ![]() geht man wie bei den einfachen
reellen Nullstellen vor.
geht man wie bei den einfachen
reellen Nullstellen vor.
Um ![]() zu berechnen, ist mit
zu berechnen, ist mit ![]() zu multiplizieren und
zu multiplizieren und ![]() zu
setzen:
zu
setzen:
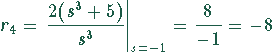
und entsprechend für ![]() :
:
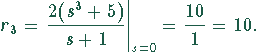
Fährt man zur Bestimmung von ![]() genauso fort, erhält
man:
genauso fort, erhält
man:
![]()
Setzt man ![]() , werden der Term auf der linken Seite und der
zweite Term auf der rechten Seite unendlich. Addiert man aber die
beiden divergierenden Terme und setzt das Resultat für
, werden der Term auf der linken Seite und der
zweite Term auf der rechten Seite unendlich. Addiert man aber die
beiden divergierenden Terme und setzt das Resultat für ![]() ein, ergibt
sich ein definierter Ausdruck, in dem
ein, ergibt
sich ein definierter Ausdruck, in dem ![]() gesetzt werden darf:
gesetzt werden darf:
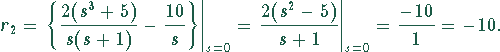
Zur Berechnung von ![]() muß man, analog wie bei der Berechnung von
muß man, analog wie bei der Berechnung von
![]() , die für
, die für ![]() divergenten Terme zusammenfassen und
die bekannten Werte
divergenten Terme zusammenfassen und
die bekannten Werte ![]() und
und ![]() einsetzten. Das ergibt
einsetzten. Das ergibt
![]() .
.
Insgesamt erhält man also die folgende Partialbruchzerlegung:
![]()
 Bei der Berechnung von Partialbruchzerlegungen mit mehrfachen
reellen Nullstellen müssen die Partialbrüche wie im Beispiel
in der richtigen Reihenfolge berechnet werden: Diejenigen Partialbrüche,
die die Nenner mit der höchsten Ordnung der
mehrfachen Nullstelle enthalten, kommen zuerst.
Bei der Berechnung von Partialbruchzerlegungen mit mehrfachen
reellen Nullstellen müssen die Partialbrüche wie im Beispiel
in der richtigen Reihenfolge berechnet werden: Diejenigen Partialbrüche,
die die Nenner mit der höchsten Ordnung der
mehrfachen Nullstelle enthalten, kommen zuerst.
 |
 |
 |
 |
 |
 |
 |
