|
|
|
|
|
|
|
|
besitzen:
wobei die Gleichung 
keine reelle Lösung
besitzt (
). Die beiden konjugiert komplexen Lösungen
lauten:
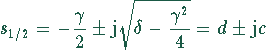
mit den Abkürzungen 
und
. Damit lautet 
faktorisiert:
Die Partialbruchzerlegung der Bildfunktion 
wird dann zu:
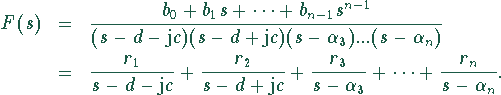
Die Berechnung der Koeffizienten 
und 
erfolgt mit der bei
den einfachen reellen Nullstellen erklärten Methode.
|
|
|
|
|
|
|
|
