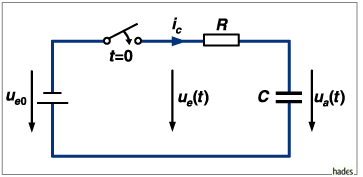
|
|
|
|
|
|
|
|
Stromkreis mit Widerstand und Kondensator
Der zeitliche Verlauf der Spannung 
am Kondensator
C soll berechnet werden mit der Anfangsbedingung
Zur Zeit 
wird die konstante Eingangsspannung
angelegt; die Eingangsspannung 
wird in diesem Fall
mit der Sprungfunktion 
beschrieben:
Für die Spannungen erhält man die Gleichung:
Die Beziehung zwischen Strom 
und der Ausgangsspannung
ist:
Einsetzen in obige Gleichung führt auf:
mit der Zeitkonstanten 
.
Dies ist eine lineare
Differentialgleichung 1. Ordnung mit konstanten Koeffizienten für die
Ausgangsspannung 
.
Die Lösung erfolgt mit Hilfe der Laplace-Transformation in drei
Schritten:
1. Transformation der Differentialgleichung in den Bildbereich:
ist dabei die Ausgangsspannung im Bildbereich,
nämlich 
.
2. Lösen der Differentialgleichung im Bildbereich:
3. Rücktransformation von 
vom Bildbereich in den
Originalbereich mit Hilfe der Transformationstabelle liefert die
gesuchte Spannung 
im Originalbereich:
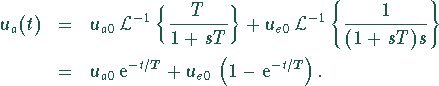
Dieses Ergebnis stimmt mit der Lösung, die man durch Trennung der Variablen im Originalbereich erhält, überein.
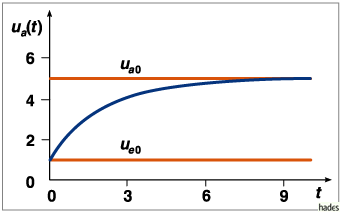
Grafische Darstellung der Ausgangsspannung 
|
|
|
|
|
|
|
|
