|
|
|
|
|
|
|
|
Arithmetisches Mittel, oft einfach Mittelwert genannt, gleichgewichtetes Mittel von n Meßwerten
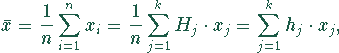
d.h., die n Meßwerte verteilen sich auf 
verschiedene 
-Werte
mit der Häufigkeit 
.
Schwerpunktseigenschaft, die Summe der Abweichungen der
Meßwerte aus der Urliste vom
arithmetischen Mittel ist durch Definition identisch Null
Linearität des arithmetischen Mittels,
Konstanten, x Meßvariable.
Quadratische Minimumseigenschaft, die Summe der Quadrate
der Abstände aller Meßwerte 
vom Mittelwert 
ist minimal:
Diese Eigenschaft ist ein Grundbestandteil der
Ausgleichsrechnung.
Vereinigung von Messungen, das Mittel einer Gesamtmessung
mit N Meßwerten
ist die Sume der Mittelwerte in den Teilmessungen, gewichtet mit dem
relativen Anteil von Meßpunkten 
.
Liegt die Meßreihe in Form einer Häufigkeitsverteilung vor,
gilt
sind in diesem Fall die Klassenmitten der Klassen 
.
|
|
|
|
|
|
|
|
