Intervallschätzung
Zur Angabe der Güte einer Punktschätzung definiert man
zwei Sorten Intervalle: das Schwankungs- oder
Prognoseintervall und das
Konfidenzintervall.
 Typisches Beispiel für eine Intervallschätzung
ist eine Waren-Ausschußprüfung:
Eine Warensendung mit
Typisches Beispiel für eine Intervallschätzung
ist eine Waren-Ausschußprüfung:
Eine Warensendung mit 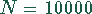 elektronischen Bauteilen soll
hinsichtlich ihres Fehleranteils
elektronischen Bauteilen soll
hinsichtlich ihres Fehleranteils 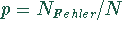 ,
d.h. des Anteils fehlerhafter
Bauelemente untersucht werden.
Natürlich werden nicht alle Teile überprüft, sondern nur eine
Stichprobe von kleinerem Umfang, z.B.
,
d.h. des Anteils fehlerhafter
Bauelemente untersucht werden.
Natürlich werden nicht alle Teile überprüft, sondern nur eine
Stichprobe von kleinerem Umfang, z.B. 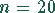 .
Das Schätzen der Ausschußrate p mittels dieser Stichprobe ist
eine Punktschätzung.
Die Bestimmung der Wahrscheinlichkeit,
mit der p in ein bestimmtes Intervall trifft, d.h. die
Güte/Genauigkeit der Schätzung, ist Gegenstand
der Intervallschätzung.
.
Das Schätzen der Ausschußrate p mittels dieser Stichprobe ist
eine Punktschätzung.
Die Bestimmung der Wahrscheinlichkeit,
mit der p in ein bestimmtes Intervall trifft, d.h. die
Güte/Genauigkeit der Schätzung, ist Gegenstand
der Intervallschätzung.
Realisation einer Schätzfunktion 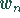 , Wert für die
Schätzfunktion
, Wert für die
Schätzfunktion 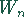 nach einmaliger Durchführung einer
Stichprobenentnahme mit Umfang n.
nach einmaliger Durchführung einer
Stichprobenentnahme mit Umfang n.
 Die Wahrscheinlichkeiten für die Anzahl
der fehlerhaften Teile in der Stichprobe des obigen Beispiels
einer Ausschußprüfung
ist gerade gegeben durch die
hypergeometrische Verteilung.
Die Schätzung des Fehleranteils p aller N Teile durch
den Fehleranteil in der Stichprobe
Die Wahrscheinlichkeiten für die Anzahl
der fehlerhaften Teile in der Stichprobe des obigen Beispiels
einer Ausschußprüfung
ist gerade gegeben durch die
hypergeometrische Verteilung.
Die Schätzung des Fehleranteils p aller N Teile durch
den Fehleranteil in der Stichprobe 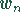 ,
so ist der Wert
,
so ist der Wert 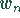 eine Realisation der Schätzfunktion
eine Realisation der Schätzfunktion
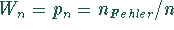 .
.
Kritischer Bereich
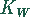 , Intervall, in das die Realisation
, Intervall, in das die Realisation
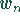 einer Schätzfunktion
einer Schätzfunktion 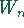 mit der Wahrscheinlichkeit
mit der Wahrscheinlichkeit
 trifft. Die Eigenschaft kritisch ist auf den Zusammenhang mit
der Testtheorie zurückzuführen, in der eine Hypothese verworfen
wird, sobald die Realisation einer Schätz-/Testfunktion in diesen
Bereich hineintrifft.
trifft. Die Eigenschaft kritisch ist auf den Zusammenhang mit
der Testtheorie zurückzuführen, in der eine Hypothese verworfen
wird, sobald die Realisation einer Schätz-/Testfunktion in diesen
Bereich hineintrifft.  ist im allgemeinen
ist im allgemeinen 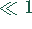 .
.
 Die Wahrscheinlichkeit dafür, maximal k fehlerhafte
Teile zu erhalten, ist gerade die Wahrscheinlichkeitssumme oder
die sogenannte
kumulative hypergeometrische Verteilung.
Wenn
Die Wahrscheinlichkeit dafür, maximal k fehlerhafte
Teile zu erhalten, ist gerade die Wahrscheinlichkeitssumme oder
die sogenannte
kumulative hypergeometrische Verteilung.
Wenn 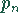 größer ist als ein vorgegebener Grenzwert
größer ist als ein vorgegebener Grenzwert 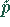 ,
soll die Warensendung abgelehnt werden. Das Intervall
,
soll die Warensendung abgelehnt werden. Das Intervall 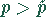 definiert also den kritischen Bereich.
definiert also den kritischen Bereich.















 Typisches Beispiel für eine Intervallschätzung
ist eine Waren-Ausschußprüfung:
Eine Warensendung mit
Typisches Beispiel für eine Intervallschätzung
ist eine Waren-Ausschußprüfung:
Eine Warensendung mit  Die Wahrscheinlichkeiten für die Anzahl
der fehlerhaften Teile in der Stichprobe des obigen Beispiels
einer Ausschußprüfung
ist gerade gegeben durch die
hypergeometrische Verteilung.
Die Schätzung des Fehleranteils p aller N Teile durch
den Fehleranteil in der Stichprobe
Die Wahrscheinlichkeiten für die Anzahl
der fehlerhaften Teile in der Stichprobe des obigen Beispiels
einer Ausschußprüfung
ist gerade gegeben durch die
hypergeometrische Verteilung.
Die Schätzung des Fehleranteils p aller N Teile durch
den Fehleranteil in der Stichprobe  Die Wahrscheinlichkeit dafür, maximal k fehlerhafte
Teile zu erhalten, ist gerade die Wahrscheinlichkeitssumme oder
die sogenannte
kumulative hypergeometrische Verteilung.
Wenn
Die Wahrscheinlichkeit dafür, maximal k fehlerhafte
Teile zu erhalten, ist gerade die Wahrscheinlichkeitssumme oder
die sogenannte
kumulative hypergeometrische Verteilung.
Wenn 






