Dormand-Prince-Verfahren

Das Dormand-Prince-Verfahren ist ein Runge-Kutta-Verfahren fünfter Ordnung.

Als Probe können die Gleichungen

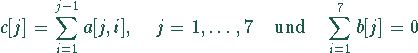
genommen werden.

program DormandPrince(input, output);

        {Integration der Gleichung y'(x) = 4*Exp(0.8x) - 0.5y(x) mittlels
        des Dormand-Prince-Verfahren}

    var
        x0, y0:   double; {Anfangswerte}
        xf:       double; {Endwert}
        h:        double; {Schrittweite}
        eps:      double; {Genauigkeit}
        x, y:     double;
        uround:   double;
        dy0, dy:  double;
        y1, hneu: double;
        nenner, fehler, faktor:    double;
        fail, accept:              boolean;
        maxit, i, j:               integer;
        b, c, k:                   array[1..7] of real;
        a:                         array[1..7,1..7] of real;

    function fxy(x, y: double): double; begin
        fxy := 4.0*Exp(0.8*x) - 0.5*y
    end; {fxy}

    procedure init; begin
       writeln('Darstellung der Loesung einer expliziten Differentialgleichung');
       writeln('mittels des Verfahren nach Dormand-Prince am Beispiel');
       writeln('y`(x) = 4*Exp(0.8x) - 0.5y(x)');
       writeln;
       writeln('Geben Sie bitte die Anfangswerte ein');
       readln(x0, y0);
       writeln('Geben Sie nun an, bis zu welchem x-Wert y(x) berechnet werden soll.');
       readln(xf);
       writeln('Und in welcher Schrittweite sollen die x-Werte liegen?');
       readln(h);
       while (xf - x0)*h < 0 do begin
           writeln('Von ', x0:1:3,' aus koennen Sie ', xf:1:3,' in Schritten von ', h:1:3,' nicht erreichen.');
           writeln('Geben Sie noch einmal den Endwert und die Schrittweite ein.');
           readln(xf, h)
       end; {while}
       writeln('Wie hoch soll die Toleranz fuer den lokalen Abschneidefehler sein?');
       readln(eps);
       while eps <= 0 do begin
           writeln('Nur positive Genauigkeiten machen Sinn. Versuchen Sie es noch einmal.');
           readln(eps)
       end; {while}
       uround := 1.0E-6;
       while (1+uround) > 1 do uround := uround*0.1;
       c[1]:=0.0;
       c[2]:=0.2;
       c[3]:=3/10;
       c[4]:=0.8;
       c[5]:=8/9;
       c[6]:=1.0;
       c[7]:=1.0;
       b[1]:=71/57600;
       b[2]:=0.0;
       b[3]:=-71/16695;
       b[4]:=71/1920;
       b[5]:=-17253/339200;
       b[6]:=22/525;
       b[7]:=-1/40;
       a[2,1]:=0.2;
       a[3,1]:=3/40;
       a[3,2]:=9/40;
       a[4,1]:=44/45;
       a[4,2]:=-56/15;
       a[4,3]:=32/9;
       a[5,1]:=19372/6561;
       a[5,2]:=-25360/2187;
       a[5,3]:=64448/6561;
       a[5,4]:=-212/729;
       a[6,1]:=9017/3168;
       a[6,2]:=-355/33;
       a[6,3]:=46732/5247;
       a[6,4]:=49/176;
       a[6,5]:=-5103/18656;
       a[7,1]:=35/384;
       a[7,2]:=0.0;
       a[7,3]:=500/1113;
       a[7,4]:=125/192;
       a[7,5]:=-2187/6784;
       a[7,6]:=11/84;
       x     := x0;
       y     := y0;
       fail  := false;
       accept:= true;
       maxit :=0;
       writeln('x       y')
    end; {init}

    procedure result; begin
        writeln( x:1:5,' ', y:1:5)
    end; {result}

    begin {Dormand-Prince}
        init;
        repeat 
            dy := 0.0;
            for j:=1 to 7 do begin
                dy0 := 0.0;
                for i:=1 to j-1 do begin
                    dy0 := dy0 + a[j,i]*k[i]
                end; {for}
                k[j] := fxy(x + c[j]*h, y + h*dy0);
                dy   := dy + b[j]*k[j]
            end; {for}
            y1 := y + h*dy0;
            if 1.0E-5 > abs(y1) then begin
                 nenner := 1.0E-5
            end else begin {if}
                 nenner := abs(y1)
            end; {if}
            if abs(y) > nenner then begin
                 nenner := abs(y)
            end; {if}
            if (2*uround/eps) > nenner then begin
                 nenner := 2*uround/eps
            end; {if}
            fehler := abs(h*dy/nenner);
            if 5.0 < (1.1*exp((1/5)*ln(fehler/eps))) then begin
                 faktor := 5.0
            end else begin {if}
                 faktor := 1.1*exp((1/5)*ln(fehler/eps))
            end; {if}
            if 1.0 > faktor then begin
                 faktor := 1.0;
            end; {if}
            hneu   := h/faktor;
            if fehler < eps then begin
                 y := y1;
                 x := x + h;
                 result;
                 if (not accept) then begin
                    if h < hneu then begin
                       hneu := h
                    end {if}
                 end; {if}
                 accept:=true;
                 maxit :=0;
            end else begin {if}
                 accept := false;
                 maxit  := maxit + 1;
                 fail   := (maxit = 20) or (x + 0.1*h = x)
            end; {if}
            h := hneu;
        until (x > xf) or fail;
    end. {Dormand-Prince}